Notes of Neural Networks

Posted on

Notes of Neural Networks

Model Representation

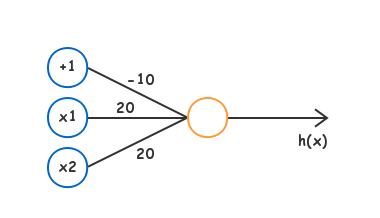
Neuron

Neural Network

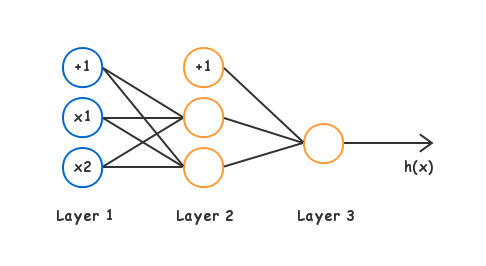
\(\begin{bmatrix} x_1 \newline x_2 \newline x_3 \newline \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \newline a_2^{(2)} \newline a_3^{(2)} \newline \end{bmatrix} \rightarrow h_\theta(x)\)

\(a^{(l)} = g(\Theta^{(l-1)} a^{(l-1)})\)

where
\(\;\;\) \(l\): index of layer
\(\;\;\) \(a^{(l)}\): "activation" in layer \(l\)
\(\;\;\) \(a_i^{(l)}\): "activation" of unit \(i\) in layer \(l\)
\(\;\;\) \(a_0^{(l)} = 1\): bias units
\(\;\;\) \(a^{(1)} = x\): input layer
\(\;\;\) \(\Theta^{(l)} \in \mathbb{R} ^ {s_{l+1} \times (s_l + 1)}\): matrix of weights
\(\;\;\) \(s_l\): number of units in layer \(l\)

Multiclass Classification

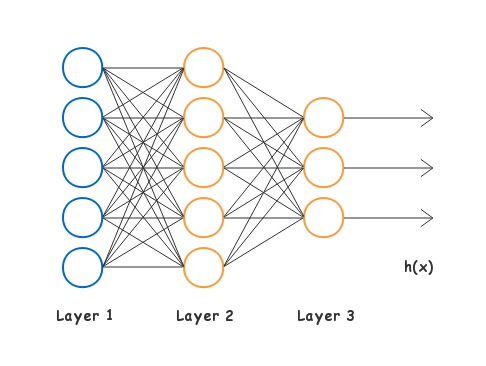
\(y \in \lbrace \begin{bmatrix} 1 \newline 0 \newline \vdots \newline 0 \end{bmatrix} , \begin{bmatrix} 0 \newline 1 \newline \vdots \newline 0 \end{bmatrix} \dots \begin{bmatrix} 0 \newline 0 \newline \vdots \newline 1 \end{bmatrix} \rbrace\)

\(h_\Theta(x) \in \mathbb{R} ^ {K}\)

\(\mathrm{prediction} = \max_k(h_\Theta(x)_k)\)

where
\(\;\;\) \(K\): number of classes

Cost Function

\(\displaystyle \begin{gather} J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[ y^{(i)}_k \log((h_\Theta(x^{(i)}))_k) + (1 - y^{(i)}_k) \log(1 - (h_\Theta(x^{(i)}))_k) \right] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} (\Theta_{j,i}^{(l)})^2 \end{gather}\)

where
\(\;\;\) \(L\): total number of layers
\(\;\;\) \(K\): number of classes / output units
\(\;\;\) \(s_l\): number of units in layer \(l\)

The double sum simply adds up the logistic regression costs calculated for each cell in the output layer The triple sum simply adds up the squares of all the individual \(\Theta\)s in the entire network

Back Propagation

Goal: \(minimize _\Theta J(\Theta)\)

Computing Partial Derivatives

TODO

Unrolling Parameters

For example, \(\Theta^{(1)} \in \mathbb{R} ^ {10 \times 11}\), \(\Theta^{(2)} \in \mathbb{R} ^ {10 \times 11}\), \(\Theta^{(3)} \in \mathbb{R} ^ {1 \times 11}\)

Unroll:

1
unrolledTheta = [Theta1(:); Theta2(:); Theta3(:)]

Reshape:

1
2
3
Theta1 = reshape(unrolledTheta(1:110), 10, 11)
Theta2 = reshape(unrolledTheta(111:220), 10, 11)
Theta3 = reshape(unrolledTheta(221:231), 1, 11)

Gradient Checking

Check that   \(\displaystyle \frac{\partial}{\partial \Theta} J(\Theta) \approx \frac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2 \epsilon}\)

where
\(\;\;\) \(\epsilon\): a small value, usually set to \(10^{-4}\)

Random Initialization

Initialize each \(\Theta_{ij}^{(l)}\) to a random value in \([-\epsilon, \epsilon]\)

where
\(\;\;\) \(\epsilon = \frac{\sqrt{6}}{\sqrt{L_{in} + L_{out}}}\)
\(\;\;\) \(L_{in} = s_l\)
\(\;\;\) \(L_{out} = s_{l+1}\)

Network Architecture

  • Number of input units = dimension of features \(x^{(i)}\)
  • Number of output units = number of classes
  • Number of hidden units per layer = usually more the better (cost of computation increases with more hidden units)
  • Number of hidden layers = defaults 1 (if ＞ 1, it is recommended to have same number of units in every hidden layer)

Summary

  1. Randomly initialize weights
  2. Implement forward propagation to get \(h_\Theta(x^{(i)})\) for any \(x^{(i)}\)
  3. Implement code to compute cost function \(J(\Theta)\)
  4. Implement back propagation to compute partial derivatives
  5. Use gradient checking to confirm that back propagation works (then disable gradient checking)
  6. Use gradient descent or advanced optimization method with back propagation to minimize \(J(\Theta)\) as a function of \(\Theta\)